 Dwa samochody wyruszyły jednocześnie naprzeciwko siebie z miejscowości A i B. Prędkość
jednego samochodu była o 30 km/h większa od prędkości drugiego samochodu. W momencie mijania
Dwa samochody wyruszyły jednocześnie naprzeciwko siebie z miejscowości A i B. Prędkość
jednego samochodu była o 30 km/h większa od prędkości drugiego samochodu. W momencie mijania
| 3 | 2 | |||
samochody przejechały odpowiednio | i | odległości między miastami. Oblicz średnie | ||
| 5 | 5 |

 ............. za momencik
............. za momencik
| ||||||||
v1= | ||||||||
| t |
| ||||||||
v2= | ||||||||
| t |
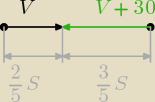 V*t = 25S (V+30)*t = 35S
ponieważ odległość i czas dla obydwu samochodów są te same porównujemy te wzory i dzielimy
przez t i S
2V = 3V+30
V1 = 60 kmh
V2 = 90 kmh
V*t = 25S (V+30)*t = 35S
ponieważ odległość i czas dla obydwu samochodów są te same porównujemy te wzory i dzielimy
przez t i S
2V = 3V+30
V1 = 60 kmh
V2 = 90 kmh

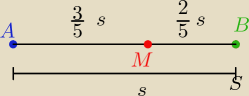 Spotkały się po tym samym czasie w punkcie M, to: t1= t2
Spotkały się po tym samym czasie w punkcie M, to: t1= t2
| 3 | ||
sam. jadący z A → B : v1 , t1, s1= | s
| |
| 5 |
| 2 | ||
sam. jadący z B → A : v2= v1 −30, t2 , s2= | s
| |
| 5 |
| v | ||
t= | ||
| s |
| v1 | ||
t1= | ||
| s1 |
| v2 | ||
t2= | ||
| s2 |
| v1 | v2 | |||
to: | = | |||
| s1 | s2 |
| 2 | 3 | |||
v1* | = ( v1−30)* | /*5
| ||
| 5 | 5 |

